Coefficiente di Strickler-Manning

Il coefficiente di Strickler-Manning, o coefficiente di Strickler, è un parametro che si usa nello studio dei flussi dei condotti, dei canali e dei fiumi; viene indicato con k_s. Nasce dalla formula di Chézy e varia rispetto alla scabrezza della superficie di riferimento.

In particolare, vale la seguente relazione:

c\cdot {\sqrt {g}}=\chi =k_{s}\cdot R^{\frac {1}{6}}

Dove:

c è un coefficiente che dà una valutazione immediata dei valori che permettono di passare dalla velocità di attrito alla portata;
g è l'accelerazione di gravità = 9,81m/s²;
R è il raggio idraulico.

L'unità di misura nel sistema internazionale è $m^{1/3}\cdot s^{-1}$ .

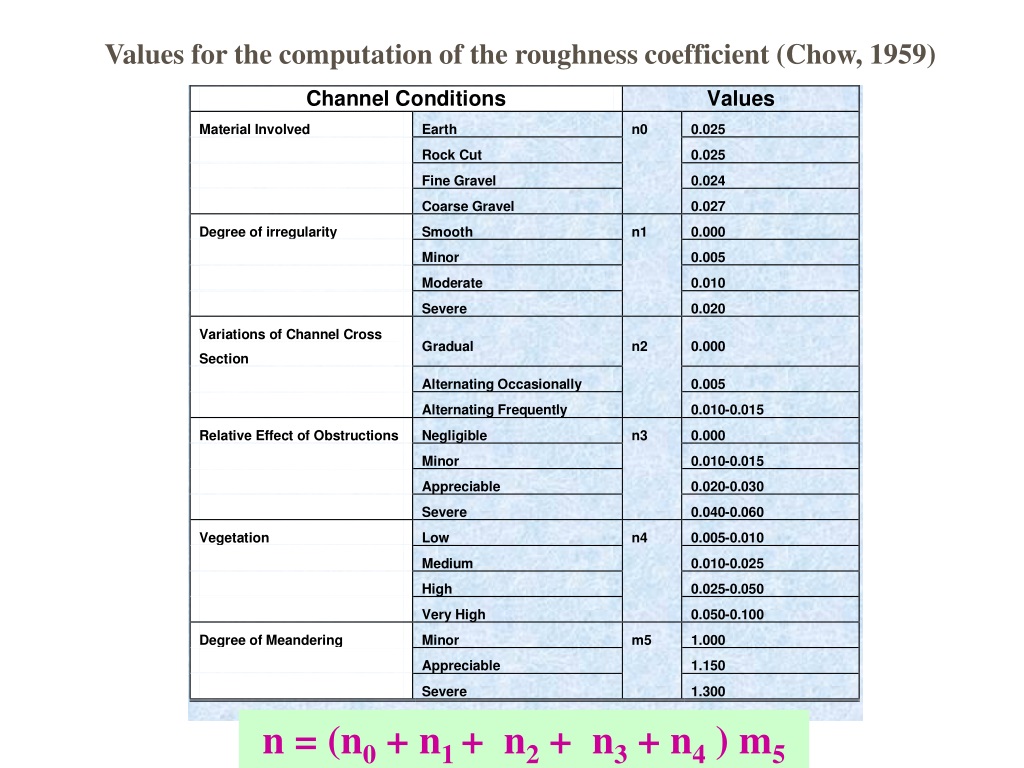
Valori significativi

Di seguito alcuni valori significativi del coefficiente di Strickler-Manning. Valori grandi di $k_{s}$ indicano una bassa scabrezza del materiale considerato.

Uso del coefficiente

Viene utilizzato per il calcolo della velocità dei fluidi. Per le condotte in pressione:

v=k_{s}\cdot R^{\frac {2}{3}}\cdot J^{\frac {1}{2}}[{\frac {m}{s}}]

Mentre per le correnti a pelo libero:

Q=A\cdot k_{s}\cdot R^{\frac {2}{3}}\cdot {\sqrt {i_{f}}}[{\frac {m^{3}}{s}}]

Dove:

Q è la portata
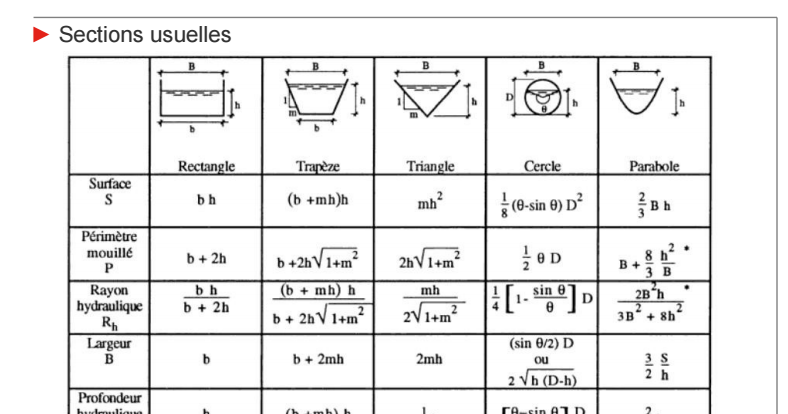
A è la l'area bagnata (A = y · b se l'alveo è rettangolare)
y è l'altezza del pelo libero
b è la larghezza dell'alveo rettangolare
R è il raggio idraulico
i_f è la pendenza del fondo (con valori minimi compresi tra 0,05% ÷ 0,1% e massimi dello 0,3%)
J rappresenta la cadente